上 扇形 弧の長さ 公式 小学生 212089

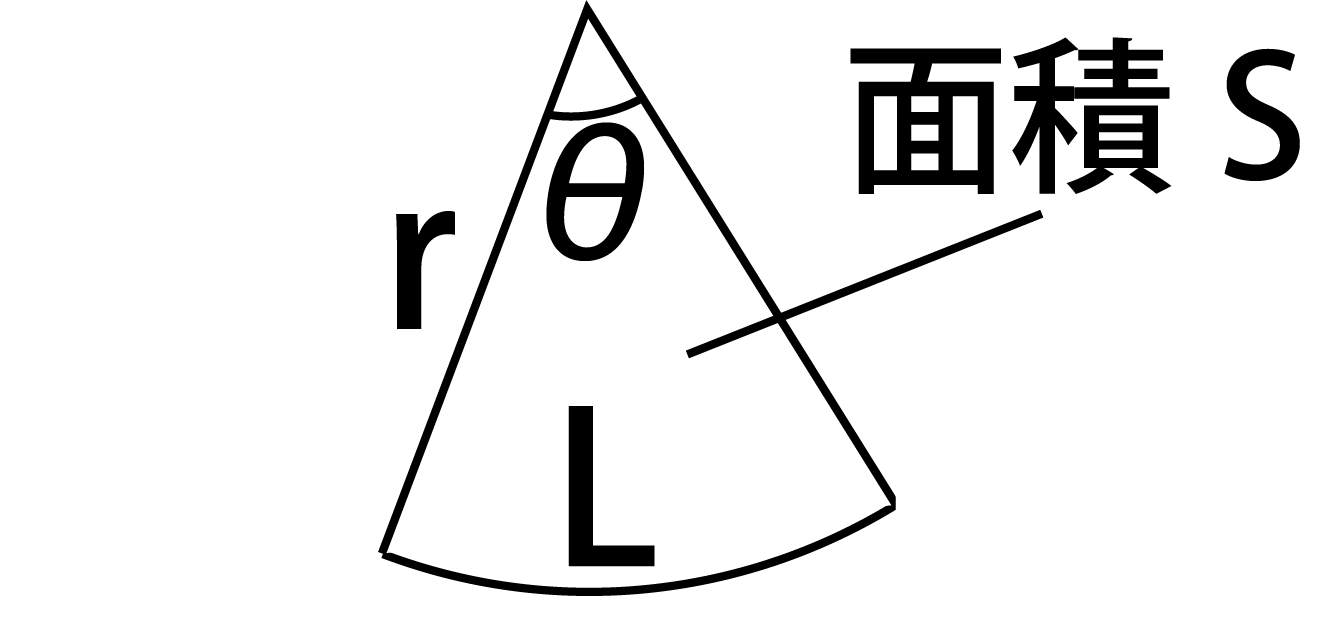
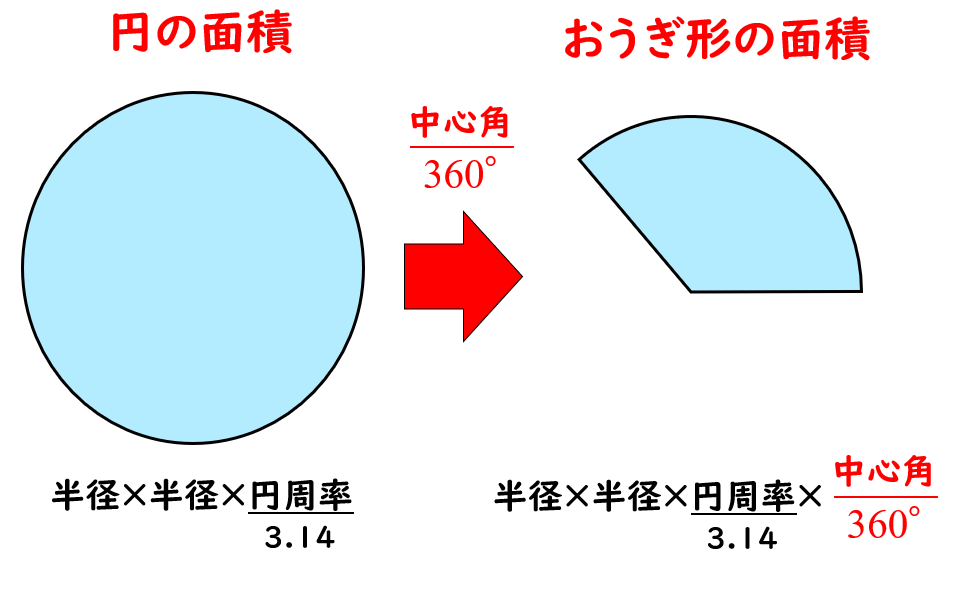
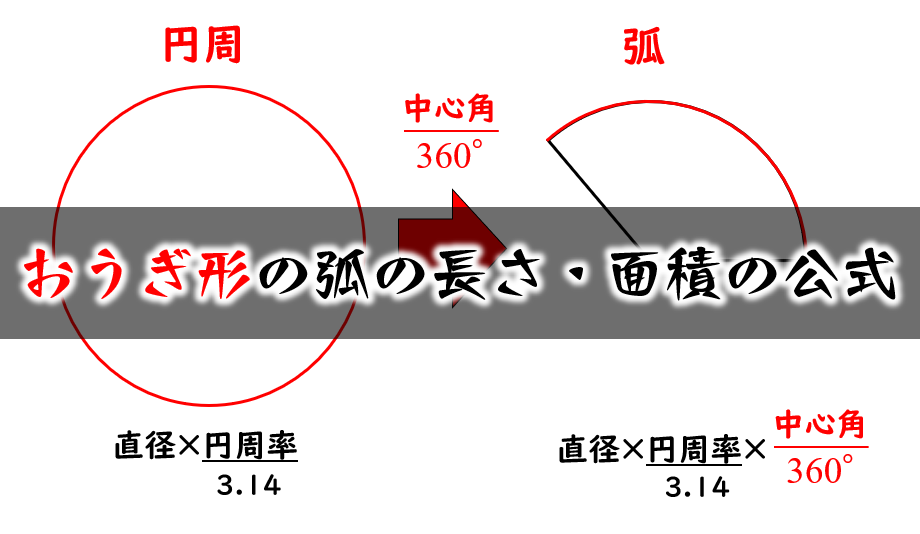
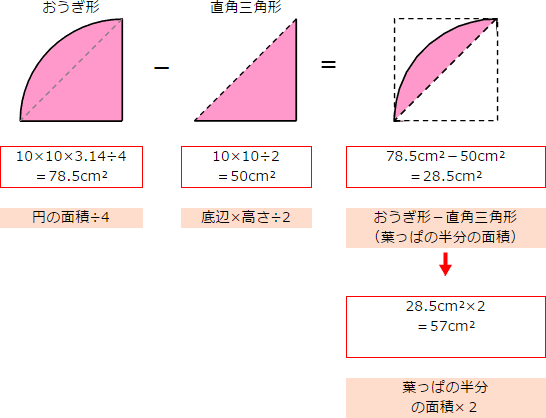
なぜ おうぎ形の面積は１ ２ 弧の長さ 半径 なのか を説明します おかわりドリル

 小学生 算数 14 ベストアンサー @hoheto_iroha 21/3/27 041 半径は半径= (弧の長さ)÷ (円周率)÷ (中心角)×180です。 弧の長さの式から導き出せますね。 (弧の長さ)= (半径)× (円周しかし、実はこの問題をはるかに簡単に解くことのできる公式が存在します。 それは、扇形の面積をS、弧の長さをl、半径をrとおくと、 S=l×r÷2 （S=lr/2） これだけです。 上の問題で試してみる

扇形 弧の長さ 公式 小学生

扇形 弧の長さ 公式 小学生-扇形の弧の長さを求める公式は、次の通りです。 l = 2πr× x 360 l = 2 π r × x 360 中心角 x°、半径 r の扇形 ここで、l は扇形の弧の長さ、π は円周率、r は円の半径、x は中心角（単位「度」）を表扇形の弧の長さ L=rθ 扇形の面積 S＝r^2θ/2＝rL/2 上式の通り、扇形の面積は、扇形の弧の長さLに半径rを掛けて2で除した値です。扇形の面積は下記が参考になります。 扇形の面積は？1分でわかる

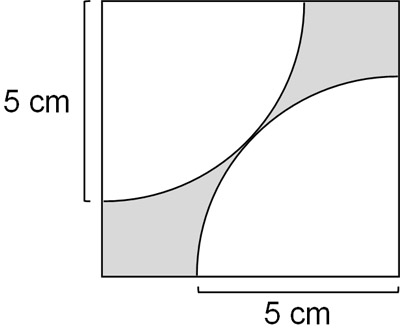
扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 Hatsudy 総合学習サイト

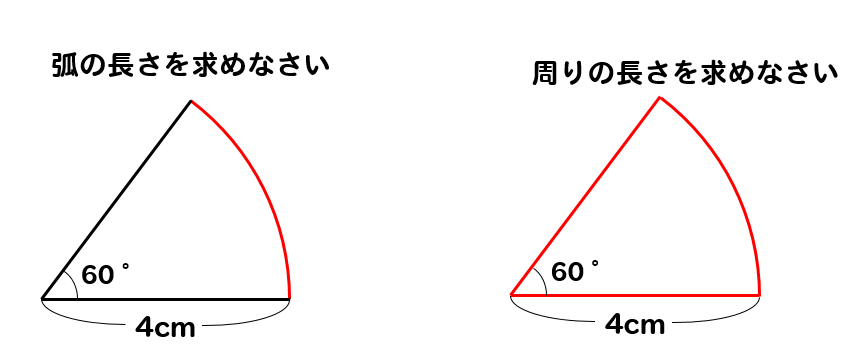
 そんな公式はありません。 円の面積、円周の長さ、又は 扇型の中心の角度の どれか 1つが分かっていないと、 扇型の弧の長さから 半径を求めることは出来ませんし、 半径から 扇「扇形の半径と弧の長さから面積を求める公式」を覚えていれば、公式に代入して S = 1 2lr = 1 2 × 4π× 3 = 6π ( = 6 ×314) ( = 14) S = 1 2 l r = 1 2 × 4 π × 3 = 6 π ( = 6 × 314) ( = 14) となり 扇形の弧の長さの公式から方程式を立てます。 l＝2πr× a 360 l ＝ 2 π r × a 360 より、 2× π× 9× a 360＝12π 2 × π × 9 × a 360 ＝ 12 π a＝240 a ＝ 240 答えは 240° 問題4 半径 8cm 8

半径 a 半径 b 扇形の面積 S 楕円弧の長さ L Elliptical Sector (1) area S =F (θ1)−F (θ0) F (θ) = ab 2 θ−tan−1( (b−a)sin2θ ba(b−a)cos2θ) r(θ)2 = a2b2 b2cos2θa2sin2θ (2) elliptical arch L= aE(面積 = 6 π c m 2 , 半径 = 4 c m 面 積 半 径 半 径 中 心 角 こ れ を 解 い て 、 度 面 積 半 径 × 半 径 × π × 中 心 角 360 ° 4 × 4 × π × a 360 ° = 6 π こ れ を 解 い て 、 a = 135 ( 度) (4) 半 小学4年生です扇型の面積、中心角、弧の長さの公式を教えてください。簡単な解き方があればそれも教えてください。 小学4年生です 扇型の面積、中心角、弧の長さの公式を教えて

扇形 弧の長さ 公式 小学生のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

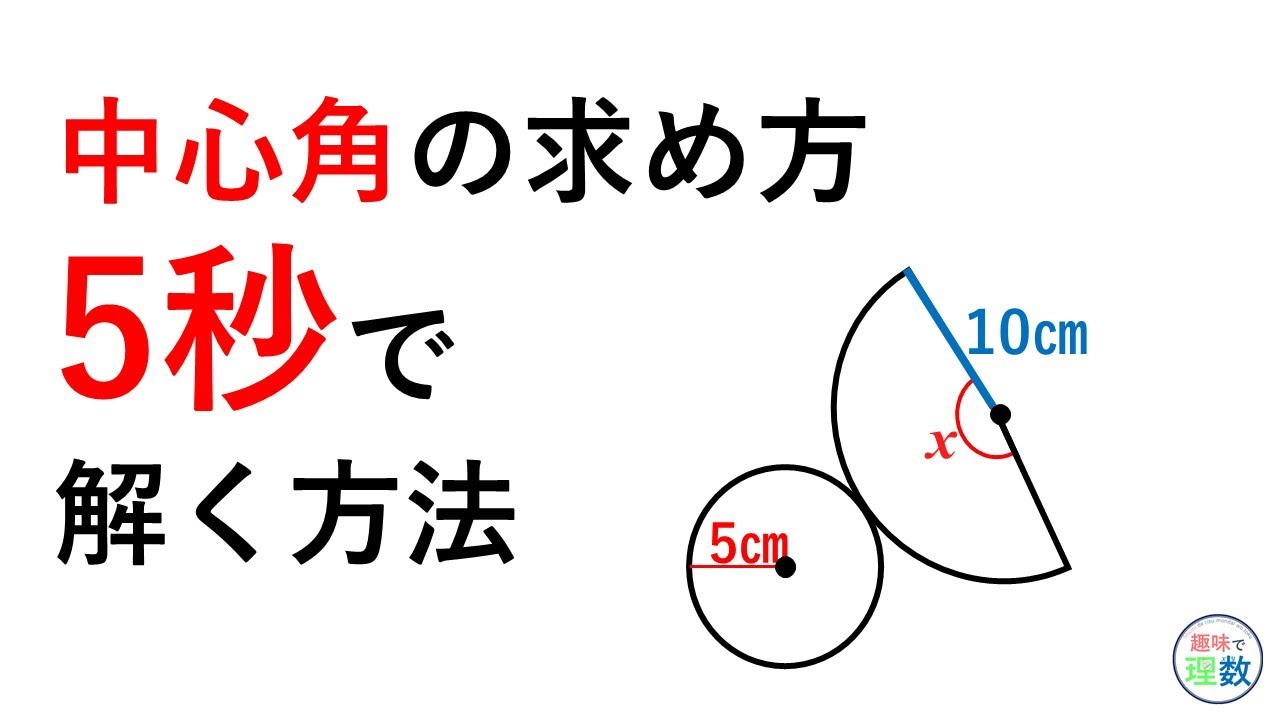
おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ
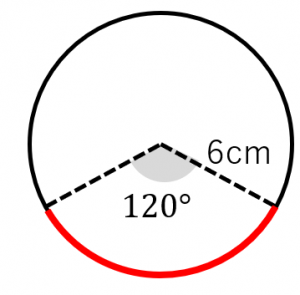おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	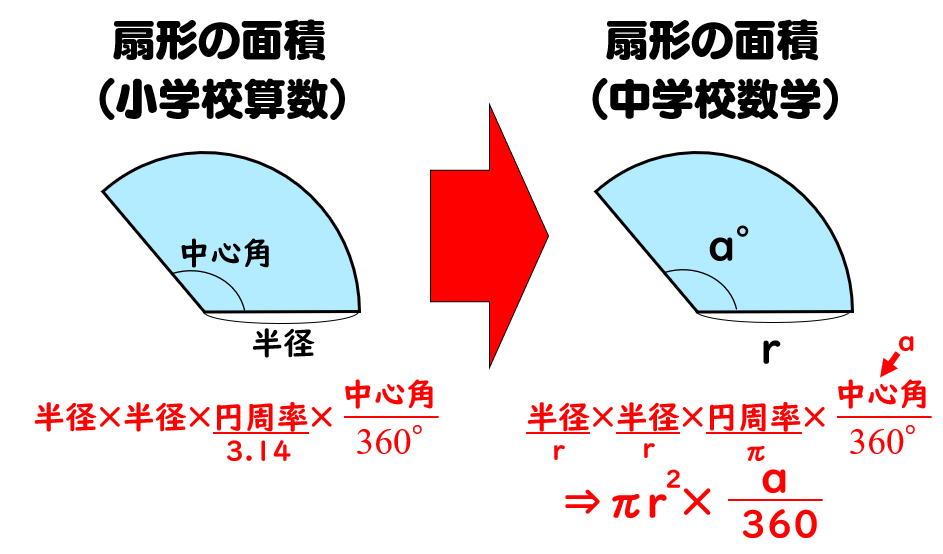おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ
おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ
おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	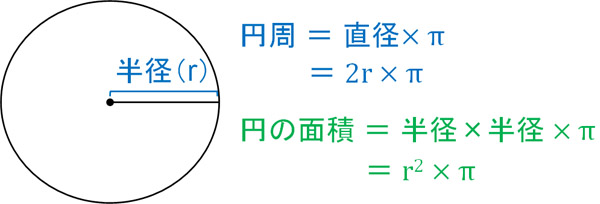おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ
おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	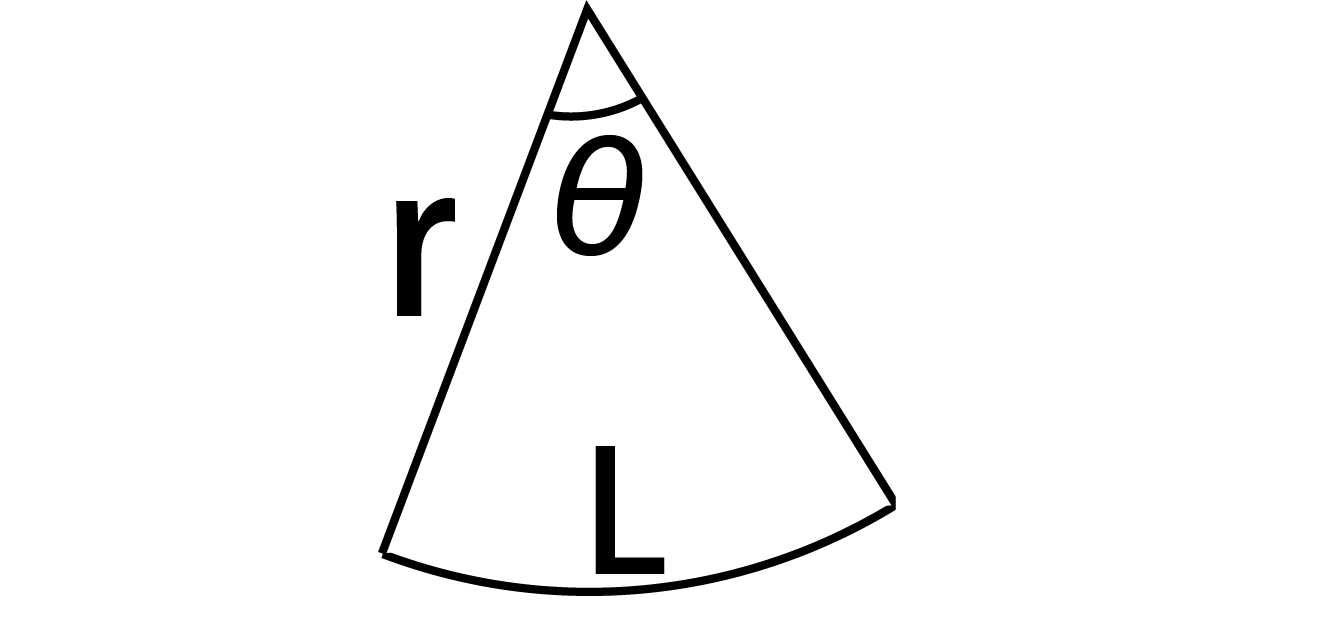おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	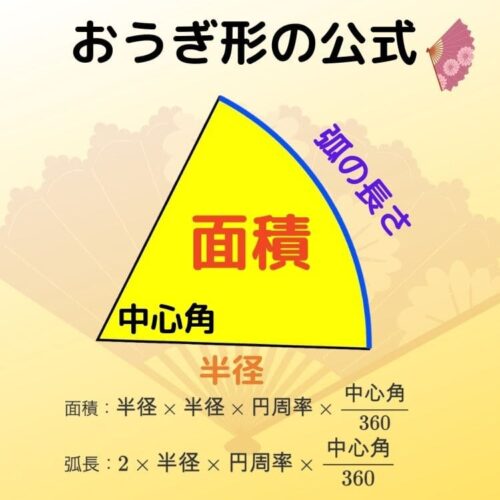おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ
おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ
おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ
おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ
おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ
おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ
おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ
おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ
おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ
おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ
おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ
おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ
おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ
おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ
おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ
おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ
おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ
おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ
おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ
おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ
おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ
おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ
おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	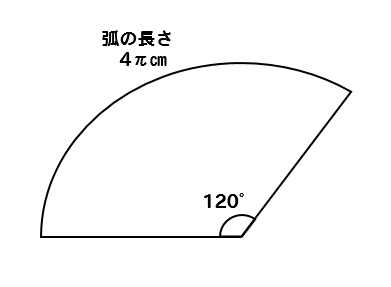おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ
おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ
おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ
おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	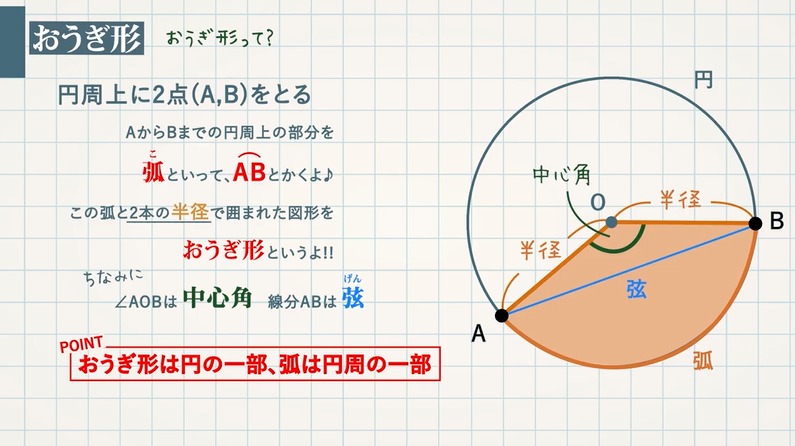おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ
おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ
おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ
おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ
おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	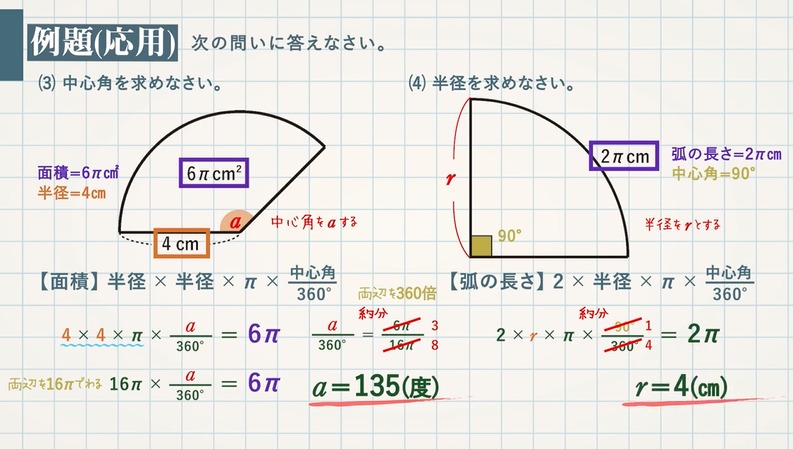おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ
おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ	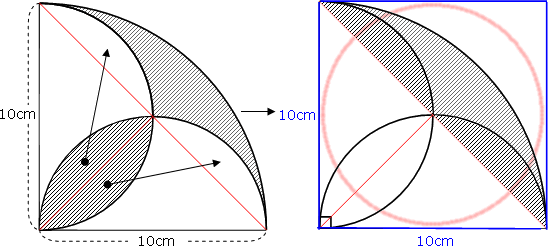おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ

 扇形の面積・弧の長さの計算機です。 角度を入力 面積は 0 π です 弧の長さは 0 π です π=とした時 面積は 0 です 弧の長さは 0 です ※円周率πは無理数ですので数は 面積の公式と弧の長さの公式を覚えていれば、新しく覚えることはありませんね。 例題はここをクリック 例題 (1) 半径 8 \text {cm} 、面積 16\pi \text {cm}^2 の扇形の中心角を求めよ。